Description
Advancement per volume or volume-specific advancement, dtrY, is related to advancement of a transformation, dtrY = dtrξ∙V-1 [MU∙L-1]. Compare dtrY with the amount of substance j per volume, cj (concentration), related to amount, cj = nj∙V-1 [mol∙V-1]. Advancement per volume is particularly introduced for chemical reactions, drY, and has the dimension of concentration (amount per volume [mol∙L-1]). In an open system at steady-state, however, the concentration does not change as the reaction advances. Only in closed systems and isolated systems, specific advancement equals the change in concentration divided by the stoichiometric number, drY = dcj/νj (closed system) drY = drcj/νj (general) With a focus on internal transformations (i; specifically: chemical reactions, r), dcj is replaced by the partial change of concentration, drcj (a transformation variable or process variable). drcj contributes to the total change of concentration, dcj (a system variable or variable of state). In open systems at steady-state, drcj is compensated by external processes, decj = -drcj, exerting an effect on the total concentration change of substance j, dcj = drcj + decj = 0 (steady state) dcj = drcj + decj (general)
Abbreviation: dtrY [MU∙L-1]
Reference: Gnaiger (1993) Pure Appl Chem, Gnaiger 2020 BEC MitoPathways
MitoPedia concepts:
Ergodynamics
MitoPedia methods:
Respirometry
Communicated by Gnaiger E (last update 2018-11-02)
Application in respirometry
- In typical liquid phase reactions the volume of the system does not change during the reaction. We define the stoichiometric number of O2 in the chemical reaction as νO2 = -1. When oxygen consumption is measured in aqueous solution in a closed system, the volume-specific oxygen flux, JV,O2, is equal to the time derivative of the advancement of the reaction per volume [1],
JV,O2 = drYO2/dt = drξO2/dt∙V-1 [(mol∙s-1)∙L-1].
- The rate of O2 concentration change is dcO2/dt [(mol∙L-1)∙s-1], where concentration is cO2 = nO2∙V-1. There is a difference between (1) JV,O2 [mol∙s-1∙L-1] and (2) rate of concentration change [mol∙L-1∙s-1]. These merge to a single expression only in a closed or isolated system (but with different sign, due to νO2 = -1. Due to external flux (O2 supply) in open systems, changes in the system concentrations differ from internal transformations (catabolic flux, O2 consumption).
From experimental to conceptual analysis
- In the experimental analysis (above), the measurement of O2 concentration change is used to calculate the flux of catabolic reactions, and corrections are applied for side reactions (such as residual oxygen consumption, ROX, and external processes,
JV,kO2 = dkYO2/dt = νO2-1· (drcO2 - dROXcO2 - decO2)/dt
- In a conceptual analysis, the question asked is What is the cause of change? Which processes or transformations cause the concentration of oxygen in the defined system to change? Clearly, it is not the change of O2 concentration over time, dcO2, that causes mitochondria to respire. On the contrary, the catabolic reactions taking place in mitochondrial electron transfer, dkcO2, are ultimately the cause of a partial change in oxygen concentration in the system, besides other internal reactions and external transfer across the system boundaries. The concentration change in the system can thus be explained by internal (i) and external (e) processes,
dcO2 = dicO2 + decO2
- The internal processes are the sum of all types of chemical reactions proceeding in the system and involving O2; the external processes are the sum of all exchange processes of O2 across the system boundaries.
- External fluxes of all substances are zero in closed systems, decO2 = 0. Although the quantities dcO2 and dicO2 are numerically identical under these conditions, that does not imply that they are conceptually identical. Even in a closed system, there is a difference between (1) the conceptual meaning of concentration change in the system, and (2) internal concentration change (partial effect of all chemical reactions, in the absence of atomic transformations).
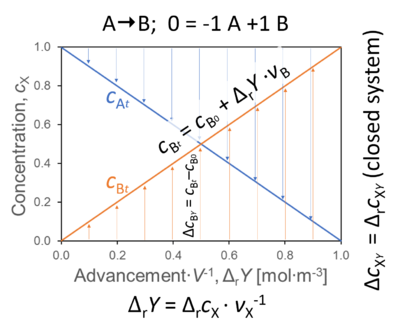
- In a closed system with a single reaction, r (A → B; 0 = -1 A +1 B), the concentration of B at time t equals (see Figure),
cBt = cB0 + ΔrY·νB
- The concentration change in B as a function of ΔrY is
ΔrcBY = cBt - cB0
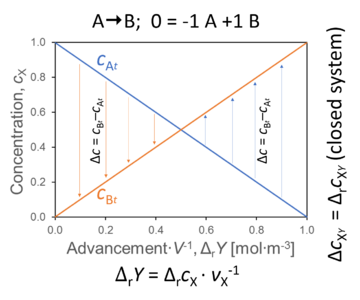
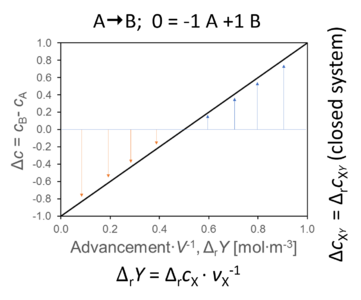
- The concentration changes of A and B over time or as a function of advancement lead to a difference of concentration between B and A (between product and substrate). The same mathematical symbol, Δ, has entirely different meaning for change versus difference,
ΔcB-A = cB - cA
From concentration and activity to chemical potential
- Bioblast links: Force and membrane potential - >>>>>>> - Click on [Expand] or [Collapse] - >>>>>>>
- Fundamental relationships
- mt-Membrane potential and protonmotive force
- O2k-Potentiometry
- » O2k-Catalogue: O2k-TPP+ ISE-Module
- » O2k-Manual: MiPNet15.03 O2k-MultiSensor-ISE
- » TPP - O2k-Procedures: Tetraphenylphosphonium
- » Specifications: MiPNet15.08 TPP electrode
- » Poster
- » Unspecific binding of TPP+
- » TPP+ inhibitory effect
- O2k-Potentiometry
- O2k-Fluorometry
- » O2k-Catalogue: O2k-FluoRespirometer
- » O2k-Manual: MiPNet22.11 O2k-FluoRespirometer manual
- » Safranin - O2k-Procedures: MiPNet20.13 Safranin mt-membranepotential / Safranin
- » TMRM - O2k-Procedures: TMRM
- O2k-Fluorometry
- O2k-Publications
References
- Gnaiger E (1993) Nonequilibrium thermodynamics of energy transformations. Pure Appl Chem 65:1983-2002. - »Bioblast link«
- Gnaiger E (2020) Mitochondrial pathways and respiratory control. An introduction to OXPHOS analysis. 5th ed. Bioenerg Commun 2020.2. - »Bioblast link«