Description
Force is an intensive quantity. The product of force times advancement is the work (exergy) expended in a process or transformation. Force times flow is power [W].
- The fundamental forces F of physics are the gravitational, electroweak (combining electromagnetic and weak nuclear) and strong nuclear forces. These gradient-forces are vectors with spatial direction interacting with the motive particle X, dmFX [N ≡ J∙m-1 = m∙kg∙s-2]. These forces describe the interaction between particles as vectors with direction of a gradient in space, causing a change in the motion (acceleration) of the particles in the spatial direction of the force. The force acts at a distance, and the distance covered is the advancement. If a force is counteracted by another force of equal magnitude but opposite direction, the accelerating effects of the two forces are balanced such that the velocity of the particle does not change and no work is done beyond the interaction between the two counteracting forces. The total net force is partitioned into partial forces, and the counteracting force may be called resistance. If the resistance is entirely due to frictional effects, then no work is done and the exergy is completely dissipated.
- Isomorphic forces can be derived from (1) the fundamental forces or (2) statistical distributions if large numbers of particles are involved. The isomorphic forces are known as 'generalized' forces of nonequilibrium thermodynamics. An isomorphic motive force, ΔtrFX, in thermodynamics or ergodynamics is the partial Gibbs (Helmholtz) energy change per advancement of a transformation (tr).
- In continuous systems accessible to the analysis of gradients, the motive vector forces, dmFX (units: newton per amount of particles X [N∙mol-1] or per coulombs of particles [N∙C-1]), are vectors interacting with the motive particles X.
- In discontinuous systems that consist of compartments separated by a semipermeable membrane, the compartmental motive forces are stoichiometric potential differences (∆) across a boundary of zero thickness, distinguished as isomorphic motive forces, ∆trFX, with compartmental instead of spatial direction of the energy transformation, tr. The motive forces are expressed in various motive units, MU [J∙MU-1], depending on the energy transformation under study and on the unit chosen to express the motive entity X and advancement of the process. For the protonmotive force the proton is the motive entity, which can be expressed in a variety of formats with different MU (coulomb, mole, or particle).
Abbreviation: F; dmFX; ΔtrFX [J·MU-1]
Reference: Gnaiger 2020 BEC MitoPathways, Gnaiger (1993) Pure Appl Chem, MitoPedia: Ergodynamics
Gibbs energy or Gibbs force?
| Gnaiger E (2018) Gibbs energy or Gibbs force? Mitochondr Physiol Network 2018-08-07. |
Abstract: Gibbs energy, G [J], is an extensive quantity, defined relative to a reference state of a system, comparable to altitude [m] defined relative to a reference (altitude at sea level). When a chemical reaction proceeds in a closed isothermal system at constant pressure, the Gibbs energy of the system undergoes a change, dG [J], when no other net transformations occur simultaneously and no work is exchanged across the system boundaries, or drG [J] when the emphasis is on the partial change of Gibbs energy due to the reaction r, irrespective of other energy transformations. In contrast to the extensive quantity of energy, force is an intensive quantity. An isomorphic force is defined as the partial derivative of Gibbs energy (exergy) per advancement of a transformation, ΔtrFX = ∂G/∂trξX. The driving force of a reaction (compare affinity), therefore, is ΔrFX = ∂G/∂rξX [J·mol-1], which may be called the Gibbs force of reaction (Gnaiger 1993).
• O2k-Network Lab: AT Innsbruck Oroboros
Physical chemistry and classical thermodynamics
- In classical thermodynamics the notion of a driving "force of chemical reactions" does not exist. Forces of chemical reactions, therefore, belong to the topic of nonequilibrium thermodynamics or ergodynamics. The "reaction Gibbs energy" is defined by IUPAC as the negative value of the "affinity of reaction", A = -ΣB νBμB (Cohen 2008 IUPAC Green Book). Since Gibbs energy is an extensive quantity expressed in the SI unit joule [J], the term "reaction Gibbs energy" suggests an extensive quantity. In fact, however, "reaction Gibbs energy" is defined as an intensive quantity expressed in the SI unit joules per mole [J·mol-1]. This nomenclature is inherently confusing (particularly when combined with #Thermodynamic ignorance), and is deeply rooted in a convention frequently applied in physical chemistry: "Unfortunately, using different symbols for extensive thermodynamic properties and their molar counterparts greatly increases the number of symbols and equations. .. Therefore, we will use a single set of symbols for thermodynamic quantities and let them represent the intensive, or molar, quantities" (Alberty 1980 Physical chemistry, p. 4).
- "It is common practice to use a single set of symbols for the extensive (Table Al) and the corresponding molar quantities. In this manner, the number of symbols is reduced. In view of the fundamental distinction between size-specific molar quantities and process-intensive molar quantities, such a simplification is acceptable only when restricted to the specific quantities. Based on the same argument and selecting a different measure of system size (mass or volume instead of amount of substance), it may be practical to use the symbols of the extensive quantities for their specific (mass- specific or volume-specific) counterparts (ref. 5). When it is necessary to discern the extensive and corresponding specific quantities explicitly, application of more complex symbols cannot be avoided (Table A2). In any case, the process-intensive quantities should be clearly distinguished from the extensive and specific properties" (Gnaiger 1993 Pure Appl Chem, p 1993).
- The adjective molar before the name of an extensive quantity generally means divided by amount of substance, n [mol]. Appart from the fact that molar has sometimes a different meaning, namely divided by amount of substance concentration, c [mol·L-1], normalization by amount of substance can lead to quantities with fundamentally different meaning (Gnaiger 1993 Pure Appl Chem):
- Normalization of an extensive quantity for amount of substance contained in the system, yields a specific quantity, comparable to a mass-specific or volume-specific quantity. In this sense, molar Gibbs energy [J·mol-1] is not an isomorphic force.
- Normalization of an extensive quantity for the amount of substance involved in an energy transformation (advancement or extent of reaction, yields an intensive quantity. Only the molar Gibbs energy in the definition of Gibbs energy change per advancement of reaction [J·mol-1] is an intensive quantity, recognized as an isomorphic force.
Ergodynamic definitions
Gibbs force of reaction
- The Gibbs force of reaction, ΔrFX (or molar Gibbs energy change of reaction of thermodynamics, ΔrGX) can be expressed in different formats and corresponding units. Most generally, ΔrFX is expressed in the molar (chemical) format as exergy per amount of reacting substance with units [J·mol-1]. It can be converted to other formats, which then are distinguished as
- ΔrFnX [J·mol-1] for the chemical format as exergy per mole of advancement of reaction,
- ΔrFeX [J·C-1] for the electrical format as exergy per coulomb of advancement of reaction
- ΔrFNX [J·x-1] for the molecular (particle) format as exergy per particle of advancement of reaction.
- The Gibbs force of reaction, ΔrFX (or molar Gibbs energy change of reaction of thermodynamics, ΔrGX) can be expressed in different formats and corresponding units. Most generally, ΔrFX is expressed in the molar (chemical) format as exergy per amount of reacting substance with units [J·mol-1]. It can be converted to other formats, which then are distinguished as
- The reaction stoichiometry of reaction r must be defined, such that the absolute value of the stoichiometric number of substance X equals 1 (νX = -1 if X is a substrate, νX = 1 if X is a product). For instance, X=A in the reaction 0 = -1 A + 2 B (glucose converted to 2 lactate), or X=B and X=C in the reaction 0 = -1/6 A - 1 B + 1 C (1/6 glucose and O2 converted to H2CO3).
- ΔrFX can be defined in different and fully consistent ways (see Supplement for derivations):
- As the difference of stoichiometric electrochemical potentials between final states (products) and initial states (reactants): The stoichiometric electrochemical potential of the substrates in reaction r is Fr,s = Σs -νs·μs; the stoichiometric electrochemical potential of the products in reaction r is Fr,p = Σp νp·μp. Therefore, the chemical force is a difference of stoichiometric electrochemical potentials, ΔrFX = Fr,p-Fr,s, where reactant X has a stoichiometric number of +1 or -1.
- As the difference of a concentration (activity)-dependent term containing the mass action ratio, and a concentration (activity)-independent term containing the apparent equilbrium constant; ΔrFX = RT ln M - RT ln K = RT ln (M/K) = RT 2.2026 (pK-pM). Defining these concentration (activity)-dependent# and indepenentX° terms as ΔrFX# = RT ln M and ΔrFX° = -RT ln K = RT ln K-1, the Gibbs force can be expressed as ΔrFX = ΔrFX#+ΔrFX°.
- As the sum of stoichiometric electrochemical potentials of all substances involved in reaction r: ΔrFB = Σi νi · μi. Definitions #1 and #3 are fully consistent, which leads to the apparent paradox, that the Δ sign in definition #3 is connected to a sum (Σ).
- As the partial derivative of Gibbs energy per advancement of reaction: ΔrFX = ∂G/∂rξX. Use of the same symbol as in definition #1 leads now in the framework of definition #4 to the apparent paradox, that a difference is defined in terms of a differential.
- ΔrFX can be defined in different and fully consistent ways (see Supplement for derivations):
Force and pressure
- Force and pressure are frequently confused. Isomorphic forces are expressed as exergy change per advancement, where the advancement is expressed in transformation-specific motive units, MU, and a variety of different formats [J∙MU-1]. In contrast, isomorphic pressures are universally expressed in the common unit of pressure, pascal [Pa]. In this formal sense, isomorphic pressure is a more fundamental concept compared to the concept of isomorphic force.
- » Pressure: the pressure-force confusion
- » Linear phenomenological laws
Thermodynamic ignorance
Nicholls DG, Ferguson SJ (2013) Bioenergetics 4. Academic Press
- "Thermodynamic ignorance is also responsible for some extraordinary errors found in the current literature, particularly in the field of mitochondrial physiology (see Part 3)." - Nicholls, Ferguson (2013): Part 3 (p 27).
- Part 3 suffers from a confusion between system and process (reaction, diffusion, transformation in general) throughout the text.
- p. 27: Distinction of three types of thermodynamic systems (isolated, closed, open) is insufficient in the context of vectorial metabolism and the protonmotive force. For explaining the nature of the protonmotive force, we need to introduce further categories of systems: homogenous systems, continuous systems with gradients, and compartmental systems with discontinuities across compartmental boundaries (discontinuous or heterogenous systems).
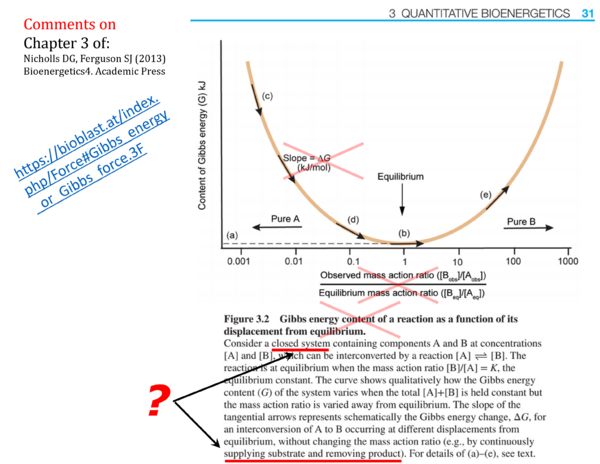
- p. 27: Open systems: The opinion that "classical equilibrium thermodynamics cannot be applid precisely to open systems because the flow or matter across their boundaries precludes the establishment of a true equilibrium" is in direct contradiction to the presentation of Figure 3.2, which attempts to explain the Gibbs energy of reaction by states maintained "by continuously supplying substrate and removing product" (p. 31).
- p. 28: "It is this displacement from equilibrium that defines the capacity of the reaction to perform useful work." - The term capacity is consfused with the term potential.
- p. 29: ".. the driving force for a reaction is an increase in entropy .." - Entropy [J·K-1] = driving force?
- p. 29: "The thermodynamic function that takes account of this enthalpy flow is the Gibbs energy change, ΔG, which is the quantitative measure of the net driving force (at constant temperature and pressure)." - Gibbs energy = net driving force ? There is a lot of confusion to be removed. What is enthalpy flow?
- p. 29: "The available energy in a gradient of ions is quantified by a further variant of the Gibbs energy change, namely the ion electrochemical gradient" - Electrochemical gradient = Gibbs energy change?
- p. 31 (Figure caption to Figure 3.2.): Gibbs energy content of a reaction as a function of its displacement from equilibrium - The term Gibbs energy content of a reaction is not consistent with IUPAC nomenclature, and the meaning of a Gibbs energy content of a reaction is unclear. The Gibbs energy of a closed system (at constant temperature and pressure; the term content is superfluous in this context) is an extensive quantity [J] that changes as a function of advancement of a reaction (which is also an extensive quantity [mol]), but this does not relate to a Gibbs energy content of a reaction.
- p. 31 (Figure 3.2.): The figure presents an inconsistency of units. The 'content of Gibbs energy (G) kJ' is plotted on the y-axis, and the x-axis is a dimensionless ratio. The slope dG/dratio, therefore, has to have the same unit as G [kJ]. Paradoxically, the Figure shows Slope = ΔG (kJ/mol). ΔG is not the "slope" in this figure. In a meaningful presentation of the concept of molar Gibbs energy change of reaction (Gibbs force [kJ/mol]) in a closed system at constant temperature and pressure, the Gibbs energy is plotted as a function of advancement of the reaction [mol].
- p. 32: "Note again that ΔG is a differential .." - As seen in Fig. 3.2, the symbol and meaning of a differential are not understood.
- Bioblast links: Force and membrane potential - >>>>>>> - Click on [Expand] or [Collapse] - >>>>>>>
- Fundamental relationships
- mt-Membrane potential and protonmotive force
- O2k-Potentiometry
- » O2k-Catalogue: O2k-TPP+ ISE-Module
- » O2k-Manual: MiPNet15.03 O2k-MultiSensor-ISE
- » TPP - O2k-Procedures: Tetraphenylphosphonium
- » Specifications: MiPNet15.08 TPP electrode
- » Poster
- » Unspecific binding of TPP+
- » TPP+ inhibitory effect
- O2k-Potentiometry
- O2k-Fluorometry
- » O2k-Catalogue: O2k-FluoRespirometer
- » O2k-Manual: MiPNet22.11 O2k-FluoRespirometer manual
- » Safranin - O2k-Procedures: MiPNet20.13 Safranin mt-membranepotential / Safranin
- » TMRM - O2k-Procedures: TMRM
- O2k-Fluorometry
- O2k-Publications
- »Bioblast links: Energy and exergy - >>>>>>> - Click on [Expand] or [Collapse] - >>>>>>>
- Units
- Joule [J]; 1 J = 1 N·m = 1 V·C; 1 cal = 4.184 J
- Units
- Fundamental relationships
- » Energy
- » Exergy
- » Extensive quantity
- Fundamental relationships
- Contrast
- » Force
- » Pressure
- » Intensive quantity
- Contrast
- Forms of energy
- » Internal-energy dU
- » Enthalpy dH
- » Heat deQ
- » Bound energy dB
- Forms of energy
- Forms of exergy
- » Helmholtz energy dA
- » Gibbs energy dG
- » Work deW
- » Dissipated energy diD
- Forms of exergy
MitoPedia concepts:
MiP concept,
Ergodynamics
Labels:
HRR: Theory