Gnaiger 2020 MitoFit x
| Gnaiger E (2021) The elementary unit — canonical reviewer's comments on: Bureau International des Poids et Mesures (2019) The International System of Units (SI) 9th ed. https://doi.org/10.26124/mitofit:200004.v2 |
» MitoFit Preprints 2020.04.v2.
Gnaiger Erich (2021) MitoFit Prep
Abstract:
- Version 2 (v2) 2021-09-06 doi:10.26124/mitofit:200004.v2
- Version 1 (v1) 2020-08-11 doi:10.26124/mitofit:200004 — »Link to all versions«
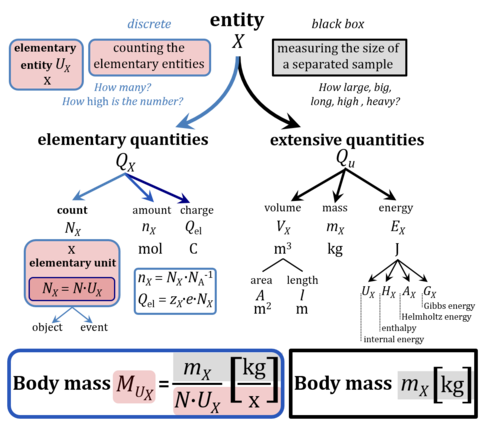
“The International System of Units, the SI, has been used around the world as the preferred system of units, the basic language for science, technology, industry and trade since it was established in 1960.” This statement heralds the 9th edition of the SI released on 2019-May-20. An new approach was introduced by defining the SI base units ― and thus the abstract SI units in general ― by their relation to fixed numerical values of fundamental constants of nature. Previous definitions of abstract units relied on a reference to concrete individual things realized as material artefacts, such as the International Prototype of the Kilogram (IPK). The (general) abstract unit ‘kilogram’ had to be calibrated in balance against an (individual) ‘entetic’ unit defining “1 kg” as a reference for the unit of mass and the mole [mol] as the unit of amount. Now the SI defines the mole as the fixed number of entities given by the Avogadro constant NA. The elementary charge e is a fixed number of charges per proton. Amount and charge are thus in a fixed relation to the count of elementary entities UX [x]. Count, amount, and charge are isomorphic elementary quantities. Amount and charge are linked to the count NX = N∙UX with elementary unit x by fixed conversion constants NA-1 [mol∙x−1] and e [C∙x−1], respectively. The SI does not use the elementary unit x. This causes a number of formal inconsistencies as discussed in the present communication on Euclid’s unit, which is UX, and Euclid’s number, which is a count NX.
• Bioblast editor: Gnaiger Erich
• O2k-Network Lab: AT Innsbruck Gnaiger E
in: Anastrophe XX Entity X and elementary unit x of A X-mass Carol
Keywords—MitoPedia
- • Amount • Avogadro constant • Concentration • Cell count • IUPAC • Density • Dimension • Elementary charge • Elementary entity • International System of Units • Mass • Number • Numeral • Unit • Volume • Quantity
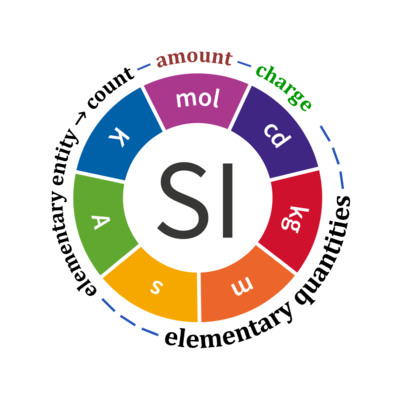
Quantity Symbol for quantity Q Symbol for dimension Name of abstract unit uQ Symbol for unit uQ [*] elementary entity *,$ UX U elementary unit x count *,$ NX = N·UX X elementary unit x amount of substance *,§ nX = NX·NA-1 N mole mol charge *,€ Qel = zX·e·NX I·T coulomb C = A·s length l L meter m mass m M kilogram kg time t T second s electric current I I ampere A thermodynamic temperature T Θ kelvin K luminous intensity Iv J candela cd
- [*] SI units, except for the canonical 'elementary unit' [x]. The following footnotes are canonical comments, related to iconic symbols.
- * For the elementary quantities NX, nX, and Qel, the entity-type X of the elementary entity UX has to be specified in the text and indicated by a subscript: nO2; Nce; Qel.
- $ Count NX equals the number of elementary entities UX. In the SI, the quantity 'count' is explicitly considered as an exception: "Each of the seven base quantities used in the SI is regarded as having its own dimension. .. All other quantities, with the exception of counts, are derived quantities" (Bureau International des Poids et Mesures 2019 The International System of Units (SI)). An elementary entity UX is a material unit, it is not a count (UX is not a number of UX). NX has the dimension X of a count and UX has the dimension U of an elementary entity; both quantities have the same abstract unit, the 'elementary unit' [x].
- § Amount nX is an elementary quantity, converting the elementary unit [x] into the SI base unit mole [mol] using the Avogadro constant NA.
- € Charge is a derived SI quantity. Charge is an elementary quantity, converting the elementary unit [x] into coulombs [C] using the elementary charge e, or converting moles [mol] into coulombs [C] using the Faraday constant F. zX is the charge number per elementary entity UX, which is a constant for any defined elementary entity UX. Qel = zX·F·nX
References
| Link | Reference | Year | View |
|---|---|---|---|
| Bureau International des Poids et Mesures 2019 The International System of Units (SI) | Bureau International des Poids et Mesures (2019) The International System of Units (SI). 9th edition:117-216. ISBN 978-92-822-2272-0 | 2019 | »Open Access« |
| Cohen 2008 IUPAC Green Book | Cohen ER, Cvitas T, Frey JG, Holmström B, Kuchitsu K, Marquardt R, Mills I, Pavese F, Quack M, Stohner J, Strauss HL, Takami M, Thor HL (2008) Quantities, Units and Symbols in Physical Chemistry. IUPAC Green Book 3rd Edition, 2nd Printing, IUPAC & RSC Publishing, Cambridge. | 2008 | Open Access |
| BEC 2020.1 doi10.26124bec2020-0001.v1 | Gnaiger E et al ― MitoEAGLE Task Group (2020) Mitochondrial physiology. Bioenerg Commun 2020.1. https://doi.org/10.26124/bec:2020-0001.v1 | 2020 | Bioenerg Commun 2020.1. |
| Hofstadter 1979 Harvester Press | Hofstadter DR (1979) Gödel, Escher, Bach: An eternal golden braid. A metaphorical fugue on minds and machines in the spirit of Lewis Carroll. Harvester Press:499 pp. | 1979 | https://en.wikipedia.org/wiki/G%C3%B6del_Escher_Bach |
| Kadosh 2015 Oxford Univ Press | Kadosh Roi Cohen, Dowker Ann, ed (2015) The Oxford handbook of numerical cognition. Oxford Univ Press:1185 pp. | 2015 | |
| Kahneman 2011 Penguin Books | Kahneman D (2011) Thinking, fast and slow. Penguin Books 499 pp. | 2011 | Penguin |
| Wilkie 2015 Front Psychol | Wilkie James EB, Bodenhausen Galen V (2015) The numerology of gender: gendered perceptions of even and odd numbers. Front Psychol 6:810. | 2015 | Front Psychol Open Access |
- Bioblast links: SI base units - >>>>>>> - Click on [Expand] or [Collapse] - >>>>>>>
- Entity, count, and number, and SI base quantities / SI base units
Quantity name Symbol Unit name Symbol Comment elementary UX elementary unit [x] UX, UB; [x] not in SI count NX elementary unit [x] NX, NB; [x] not in SI number N - dimensionless = NX·UX-1 amount of substance nB mole [mol] nX, nB electric current I ampere [A] A = C·s-1 time t second [s] length l meter [m] SI: metre mass m kilogram [kg] thermodynamic temperature T kelvin [K] luminous intensity IV candela [cd]
- Fundamental relationships
- » Avogadro constant NA
- » Boltzmann constant k
- » elementary charge e
- » Faraday constant F
- » gas constant R
- » electrochemical constant f
- Fundamental relationships
- SI and related concepts
Preprints for Gentle Science
» MitoFit Preprints - the Open Access preprint server for mitochondrial physiology and bioenergetics
Cited by
- Gnaiger E (2021) Bioenergetic cluster analysis – mitochondrial respiratory control in human fibroblasts. MitoFit Preprints 2021.8. https://doi.org/10.26124/mitofit:2021-0008
- Gnaiger E (2020) Mitochondrial pathways and respiratory control. An introduction to OXPHOS analysis. 5th ed. Bioenerg Commun 2020.2. https://doi.org/10.26124/bec:2020-0002
Labels: MiParea: Respiration
Organism: Human
BME, Amount of substance, Avogadro constant, Concentration, Count, Density, Dimension, Elementary charge, Elementary entity, Entity, International System of Units, Mass, Number, Numeral, Unit, Volume, Quantity, BEC 2020.2, MitoFit 2021 BCA